Закон всемирного тяготения

Закон всемирного тяготения

Две материальные точки, обладающие массами m₁ и m₂, притягиваются друг к другу с силой F:

1)

где

• R — расстояние между точками;
• γ — гравитационная постоянная (может иметь обозначение G или G_N), равная 6,6720·10^-11 Н·м²/кг² (система СИ), 6,67·10^-8 см³/г·с² (система СГС).

Гравитационная постоянная есть величина, численно равная силе притяжения двух материальных точек, имеющих массы, равные единице, находящихся на единичном расстоянии. В случае однородных шаров с массами m₁ и m₂ сила взаимодействия выражается той же формулой, причем R означает расстояние между центрами шаров.

Сила притяжения между телом массы m, расположенным на поверхности Земли, и Землей

2)

где

• М_З — масса Земли;
• R_З — радиус земного шара.

Все тела в данной точке Земли падают с одинаковыми ускорениями относительно ее поверхности. Это ускорение при свободном падении обозначается обычно буквой g. Вследствие суточного вращения Земли ускорение g будет обусловлено векторной суммой двух сил: силой притяжения Земли F (формула 2) и центростремительной силой F_ц (формула 6). Равнодействующая этих сил называется силой тяжести.

Сила тяжести тела с массой m определяется следующим выражением:

3)

Сила тяжести P и сила притяжения к Земле F отличаются (незначительно) друг от друга по величине и по направлению. Угол α между направлениями сил P и F (фиг.1) на широте φ:

α = 0,0018 sin 2φ

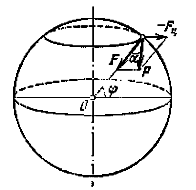
Направление P совпадает с направлением отвеса; сила притяжения F всегда направлена к центру Земли; обе силы совпадают по направлению лишь на полюсах, где P=F, и на экваторе, где P=F–F_ц.

Вследствие этого и ввиду отличия Земли от шарообразной формы ускорение силы тяжести зависит от широты.

Ускорение силы тяжести (напряженность поля тяготения), в соответствии с законом тяготения, на высоте H от поверхности Земли выражается формулой

4)

где

• g₀ — ускорение на поверхности Земли.

В первом приближении при HR_З

5)

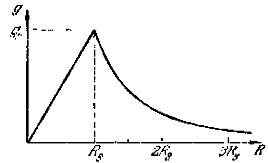
В центре Земли напряженность поля тяготения равна нулю. Если Землю принять за однородный шар, то по мере удаления от центра Земли g растет. Вне Земли по мере удаления от центра Земли g убывает; зависимость ускорения g от расстояния до центра Земли изображена графиком (фиг.2).

Литература