Статика рассматривает условия равновесия тела или системы тел. Если на покоящееся тело действует несколько сил, направления которых пересекаются в одной точке, то оно останется в покое тогда, когда сумма (векторная) этих сил равна нулю. Точку приложения силы можно смещать вдоль линии ее действия.
Центр тяжести твердого тела или системы тел
На каждую частицу тела действует сила тяжести. Точка, в которой приложена равнодействующая сил тяжести, действующих на отдельные точки тела, называется центром тяжести. Сумма моментов сил тяжести всех частиц тела относительно центра тяжести равна нулю.
Виды равновесия тел
Если при достаточно малом отклонении тела от положения равновесия возникают силы, стремящиеся вернуть тело в первоначальное положение, то такое равновесие называется устойчивым.
Обычно после действия малых возмущений (смещений, толчков) на тело, находящееся в устойчивом равновесии, оно начинает совершать колебания с малой амплитудой около положения равновесия; эти колебания затем затухают вследствие трения и равновесия восстанавливается.
В положении устойчивого равновесия потенциальная энергия тела имеет минимальное значение (при действии консервативных сил).
Если же при сколь угодно малом отклонении тела от положения равновесия возникают силы, стремящиеся увеличить это отклонение, то такое положение называют неустойчивым.
В безразличном положении равновесия при отклонении тела не возникает никаких сил, и новое положение также является положением равновесия.
Условия равновесия на наклонной плоскости
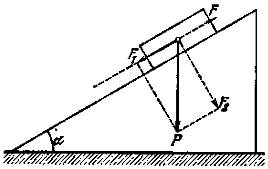
Для равновесия тела, имеющего вес P, на наклонной плоскости, составляющей угол α с горизонтом, нужно приложить силу F, равную F1, причем F1=Psinα сила F должна быть направлена вдоль наклонной плоскости (фиг.1). При этом тело давит на наклонную плоскость с силой F2=Psinα, а наклонная плоскость с такой же силой действует на лежащее на ней тело. Свободно лежащее тело будет покоится на наклонной плоскости, пока скатывающая сила не станет больше силы трения покоя. Это произойдет, когда tgα > k, где k – коэффициент трения покоя.
Рычаг
Рычаг находится в равновесии, если векторная сумма моментов действующих на него сил равна нулю (фиг.2).
F1a – F2b=0
где
- a и b — плечи сил F1 и F2.

а) рычаг с точкой опоры, находящейся между точками приложения действующих на него сил; б) рычаг, в котором точки приложения действующих сил находятся по одну сторону от точки опоры
Условия равенства моментов сил применяются также к равновесия ворота (фиг.3,а) или лебедки.
Блоки
Неподвижный блок (фиг.3,б) служит только для изменения направления действующей силы. Подвижный блок (фиг.3,в) позволяет получить выигрыш в силе. При покоящемся или равномерно вращающемся подвижном блоке сумма всех действующих сил и сумма всех моментов сил равны нулю.
Отсюда следует, что
P = 2F, или F = P/2.

а) ворота; б) неподвижного блока; в) подвижного блока
Полиспаст
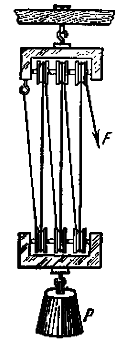
Полиспаст (фиг.4) представляет собой систему подвижных и неподвижных блоков, соединенных в общем держателе. Если полиспаст имеет n подвижных и n неподвижных блоков, то сила F, уравновешивающая силу P, равна F = P/2n.
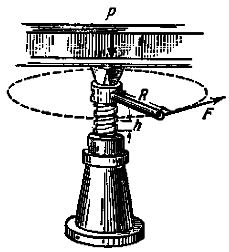
При отсутствии трения сила P, действующая по оси винта, уравновешивается силой F, приложенной к рукоятке (фиг.5):
F = Ph/2πR,
где
- R — расстояние от оси вращения до точки приложения силы;
- h — шаг винта.
Приложение

| Тело | Положение центра тяжести |
|---|---|
| Тонкий стержень | На середине стержня |
| Цилиндр или призма | На середине прямой, соединяющей центры оснований цилиндра или призмы |
| Шар | В центре |
| Плоский сегмент малой толщины | На оси симметрии, смещен от основания на 2/5 его высоты |
| Пирамида или конус | На отрезке, соединяющем вершину с центром основания; смещен на ¼ этого отрезка |
| Полушарие | На оси симметрии, смещен от центра на 3/8 радиуса |
| Сплошная треугольная пластина малой толщины | В точке пересечения медиан |
Литература
- 53 просмотра