Кинематика изучает движение тел, не рассматривая причин, вызывающих это движение.
Простейшим движущимся телом является материальная точка. Материальной точкой называется тело, размерами которого можно пренебречь при описании его движения. Например, годичное движение Земли вокруг Солнца можно представлять как движение материальной точки, а суточное вращение Земли вокруг своей оси – уже нельзя.
Всякое твердое тело можно рассматривать как систему жестко связанных друг с другом материальных точек.
Линия, описываемая движущейся материальной точкой, называется траекторией. Движения разделяются по виду траектории на прямолинейные (траектория – прямая) и криволинейные (траектория – кривая). По своему характеру движение может быть равномерным или переменным.
Прямолинейное движение
Равномерным движением называется движение, при котором точка в любые равные промежутки времени проходит равные расстояния; в противном случае движение называется переменным. Скоростью равномерного движения (v) называется величина, измеряемая длиной дуги (s), проходимого в единицу времени (t):
1)
![]()
В случае переменного движения различают мгновенную и среднюю скорости. Если за время от момента t0 до момента t0+Δt тело пройдет путь Δs, то отношение
2)
![]()
называется средней скоростью за промежуток времени Δt.
Мгновенной скоростью, или скоростью в данный момент времени t0, называется предел
3)
![]()
Скорость – величина векторная. Сложение скоростей производится по правилу параллелограмма (векторно). Единицы скорости: см/с (СГС), м/с (СИ) и внесистемные единицы км/с, км/ч.
Движение, в котором за любые равные промежутки времени скорость изменяется на одинаковую величину, называется равнопеременным. Величина, численно равная изменению скорости, называется ускорением (a); точнее
4)
![]()
где
- vt — скорость в момент времени t;
- v0 — скорость в момент начала отсчета времени t0.
Ускорение является также векторной величиной. Единицами измерения ускорения служат: см/с2, м/с2, км/с2.
Скорость равнопеременного движения в любой момент времени
5)
![]()
где
- v0 — скорость в момент начала отсчета времени.
Ускорение может быть как положительным (ускорение движения), так и отрицательным (замедленное движение).
Путь, пройденный за время t при равнопеременном движении:
6)
![]()
В равнопеременном движении скорость в конце пройденного пути может также определятся начальной скоростью движения, ускорением и пройденным путем:
![]()
Частным случаем прямолинейного движения с постоянным ускорением является падение тел с небольшой высоты (много меньшей радиуса Земли). Обозначив высоту для свободного падения (v0=0) через h, а ускорение падающих тел через g, имеем
7)
![]()
- t — время падения.
Вращательное движение
Круговым движением точки около некоторой оси называется такое движение, при котором траекторией точки является окружность с центром на этой оси, причем плоскость окружности перпендикулярна к этой оси.
Вращательным движением тела вокруг некоторой оси называется такое движение, при котором все точки тела совершают круговое движение около этой оси.
Равномерным вращением называется такое движение, при котором тело за любые равные промежутки времени поворачивается на один и тот же угол.
Угловая скорость равномерного вращения (ω) есть величина, измеряемая углом поворота за единицу времени:
8)
![]()
где
- ω — угол поворота за время t, измеряемый в радианах (рад).
Угловая скорость может быть выражена через число оборотов в единице времени n или период обращения T:
9)
![]()
10)
![]()
Линейной скоростью точки во вращательном движении называется мгновенная скорость движущейся точки. Вектор скорости направлен по касательной к траектории. Угловая скорость ω связана с линейной скоростью v:
11)
![]()
где
- R — расстояние от точки до оси вращения.
12)
![]()
Предел этого отношения есть, по определению, мгновенная угловая скорость в момент времени t0:
13)
![]()
Вращение, при котором за любые равные промежутки времени угловая скорость изменяется на одну и ту же величину, называется равнопеременным.
Угловым ускорением равнопеременного вращения ε называется величина, измеряемая изменением угловой скорости в единицу времени; точнее
14)
![]()
где
- ωt — угловая скорость в момент времени t;
- ω0 — угловая скорость в момент начала отсчета времени t0.
Угловая скорость ω и угловое ускорение ε – величины векторные; направление вектора ω определяется по правилу правого винта (фиг.1): если головку винта вращать по направлению вращения тела, то поступательное движение винта будет совпадать с направлением ω; вектор ω направлен вдоль оси вращения. Направление вектора углового ускорения совпадает с направлением ω, если угловая скорость увеличивается; при уменьшении угловой скорости направление вектора ε противоположно направлению ω.

Если равнопеременное вращательное движение характеризовать числом оборотов в единицу времени n, то можно ввести ускорение ε*:
15)
![]()
- nt — число оборотов в момент времени t;
- n0 — число оборотов в момент начала отсчета времени t0.
Угловая скорость равнопеременного вращения и частота оборотов по истечении времени t после начала вращения равны
16)
![]()
Угол поворота при равнопеременном вращении и число оборотов:
17)
![]()
При движении тела по криволинейной траектории скорость изменяется не только по величине, но и по направлению (фиг.2).
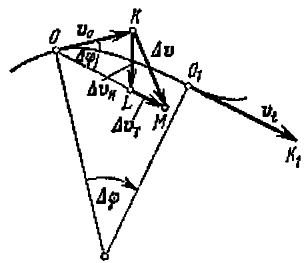
Ускорения a, aт, aн будут равны соответствующим изменениям скорости за единицу времени)
Изменение величины линейной скорости за единицу времени называется тангенциальным ускорением:
18)
![]()
или, более строго,
19)
![]()
где
- vt и v0 — величины линейных скоростей в моменты времени t0+Δt и t0.
Тангенциальное ускорение связано с угловым ускорением:
20)
![]()
Направление aT в данной точке траектории совпадает с направлением скорости или противоположно ему.
Изменение скорости по направлению за единицу времени называется нормальным ускорением:
21)
![]()
или, более строго,
22)
![]()
Нормальное ускорение направлено по радиусу кривизны траектории (к оси вращения).
Например, при равномерном вращении тела точки его движутся с ускорением, так как направление их скорости все время меняется. Нормальное ускорение в этом случае направлено к оси вращения (т.е. перпендикулярно к направлению линейной скорости) и носит название центростремительного ускорения:
23)
![]()
где
- v — линейная скорость;
- ω — угловая скорость;
- R — радиус вращения точки.
Полное ускорение точки тела при равнопеременном вращательном движении (фиг.2).
24)
![]()
Движение тел в земном поле тяготения
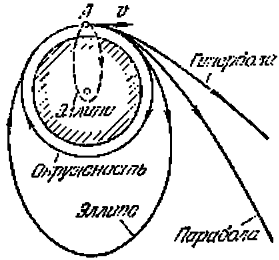
На фиг.3 показаны траектории тел, вылетевших из точки A, лежащей вблизи поверхности Земли, с различными скоростями (сопротивление воздуха не учитывается). Во всех случаях скорость направлена горизонтально. Траекторией тела является окружность, если скорость тела v в точке A такова, что ускорение свободного падения g равно центростремительному ускорению v2/R (R – радиус траектории, который при небольшой высоте можно принять равным радиусу земного шара). Отсюда
![]()
Эта величина называется первой космической скоростью.

Если скорость тела в точке A больше 7,93 км/с, но меньше 11,1 км/с, то траектория тела представляет собой эллипс, причем его фокус, ближайший к точке вылета, находится в центре Земли (на фиг.3 этот эллипс изображен сплошной линией). Если скорость тела равна 11,16 км/с – второй космической скорости, то его траектория – парабола. При начальной скорости, большей 11,16 км/с, траектория тела станет гиперболой. В последних двух случаях тело покинет Землю и уйдет в межпланетное пространство. Наименьшую скорость, при которой тело покинет Землю, иногда называют скоростью убегания (или скоростью освобождения). При движении тела со скоростями, меньшими 7,93 км/с, траектории движущегося тела представляют собой отрезки эллипса (изображенного на фиг.3 пунктиром), дальний фокус которого совпадает с центром Земли.
При движении со скоростями меньшими 7,93 км/с, эти отрезки можно считать отрезками парабол.
Если тело брошено с поверхности Земли под углом α с начальной скоростью v0, значительно меньшей 7,93 км/с, то ускорение свободного падения также можно считать постоянным как по величине, так и по направлению, а поверхность Земли рассматривать как плоскую. В этом случае траекторией является парабола (фиг.4), а дальность полета (S) и наибольшая высота подъема (H) вычисляются по формулам:
25)
![]()
где
- v0 — скорость вылета тела.
Одна и та же дальность полета может быть получена при двух значениях угла бросания: α1 и α2, причем α2=90°–α1.
Максимальной дальности полета соответствует угол α=45°.
При наличии сопротивления воздуха дальность полета и высота подъема уменьшаются. Если, например, при отсутствии сопротивления воздуха, угле бросания α=20° и начальной скорости v0=550 м/с тело имело бы дальность полета 19,8 км, то снаряд, движущийся в воздухе при таких же значениях начальной скорости и угла бросания, имеет дальность полета всего 8,1 км.
Приложение
| Ускоренное движение | Ускорение, м/с2 |
|---|---|
| Поезд метро | 1 |
| Поезд пассажирский | 0,35 |
| Гоночный автомобиль | 4,5 |
| Скоростной пассажирский лифт | 0,9-1,6 |
| Трамвай | 0,6 |
| Запуск ракеты | 30-90 |
| Снаряд в стволе орудия | 100 000 |
| Ускоренное движение | Ускорение, м/с2 |
| Замедленное движение | Ускорение (отриц.), м/с2 |
| Аварийное торможение автомобиля | 4-6 |
| Реактивный самолет при посадке | 5-8 |
| Планеты | Период обращения вокруг Солнца (ТС), (в годах) |
Период обращения вокруг оси (Т0) | Орбитальная скорость (v0), км/c |
Скорость освобождения (v), км/c |
Число спутников (N) |
|---|---|---|---|---|---|
| Меркурий | 0,241 | 88 дней | 48,8 | 4,2 | — |
| Венера | 0,615 | 247±5 дней | 35,0 | 10,2 | — |
| Земля | 1,00004 | 23 ч 56 мин 4 сек | 29,8 | 11,16 | 1 |
| Марс | 1,881 | 24 ч 37 мин 23 сек | 24,2 | 5,01 | 2 |
| Юпитер | 11,86 | 9 ч 51 мин | 13,06 | 59,5 | 12 |
| Сатурн | 29,46 | 10 ч 14 мин | 9,65 | 35,4 | 9 |
| Уран | 84,01 | 10 ч 49 мин | 6,78 | 22,2 | 5 |
| Нептун | 164,8 | 14 ч (?) | 5,42 | 24,8 | 2 |
| Плутон | 247,7 | — | 4,73 | — | — |
| Луна | (спутник Земли) | 27 дней 7 ч 43 мин 11 сек | — | 2,37 | — |
| Высота (H), 103км | Скорость убегания (v), км/c |
|---|---|
| 0 | 11,19 |
| 0,5 | 10,77 |
| 1 | 10,40 |
| 2 | 9,76 |
| 5 | 8,37 |
| 10 | 6,98 |
| 20 | 5,50 |
| 30 | 4,68 |
| 40 | 4,15 |
| 50 | 3,76 |
| Высота (H), км | Период обращения (Т), ч |
|---|---|
| 0 | 1,41 |
| 250 | 1,49 |
| 500 | 1,58 |
| 750 | 1,68 |
| 1000 | 1,75 |
| 1500 | 1,93 |
| 1690 | 2,00 |
| 2000 | 2,12 |
| 5000 | 3,35 |
| 10000 | 5,78 |
| 35800 | 23,935 |
Литература
- 237 просмотров